Following Gilbert Strang 4
벡터 공간에 관해서 알아보자.
Vector Spaces
- Spaces is “bunch of something,” in this case, vector
- Adding between members and multiplying scalar also produces a member in the space.
벡터 공간 $V$에 대해서, $w, v \in V$일 때, $\alpha, \beta \in \mathbb R$, 일 때 $\alpha w + \beta v \in V$을 만족하면 $V$는 벡터 공간이다.
- 벡터 공간 안의 두 원소를 더한 것이 벡터 공간에 속해야 한다.
- 원소에 스칼라 곱을 한 것이 벡터 공간에 속해야 한다.
- 부분 공간이란 어떤 벡터 공간 안에 들어가 있는 또다른 벡터 공간을 의미한다.
- 부분 공간 자체로 벡터 공간이 되어야 하기 때문에 ${ 0 }$를 반드시 지니고 있어야 한다.
- 어떤 유한한 공간은 벡터 공간이 될 수 없다.
Subspaces
- A vector space inside $\mathbb R^2$.
- $\mathbb R^2$ 평면 안에 들어간 수직선을 생각하자.
- 부분 공간은 그 자체로서 vector spaces로서 성립해야 한다.
Three question to be checked
- 출처를 확인해도 된다.
$$
x_1 =
\begin{bmatrix}
0 \\
1 \\
3 \\
\end{bmatrix},~
x_2 =
\begin{bmatrix}
2 \\
4 \\
0 \\
\end{bmatrix}
$$
- $x_1$과 $x_2$가 생성하는 부분공간 $V_1$, $V_2$를 찾고, $V_1 \cap V_2$를 찾아보자.
- ${ x_1, x_2 }$가 생성하는 부분공간 $V_3$를 찾아보자. 이는 $V_1 \cup V_2$과 일치하는가?
- $V_3$의 어떤 부분공간을 $S_3$라고 할 때 $x_1 \notin S_3$ and $x_2 \notin S_3$인 $S_3$가 존재하는가?
- $V_3$와 $x-y$ 평면의 교점은 존재하는가?
Q1
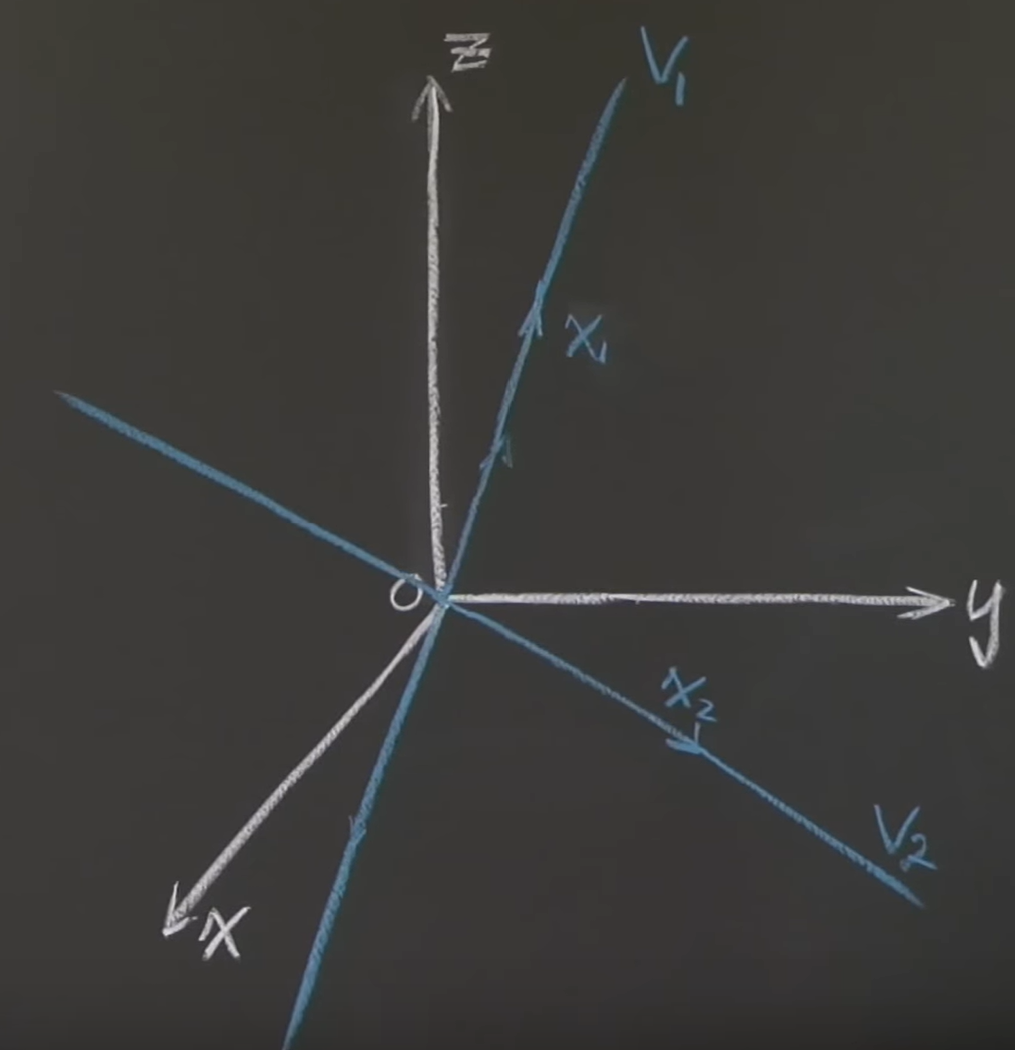
$$
V_1 \cap V_2 = \{0\}
$$
Q2
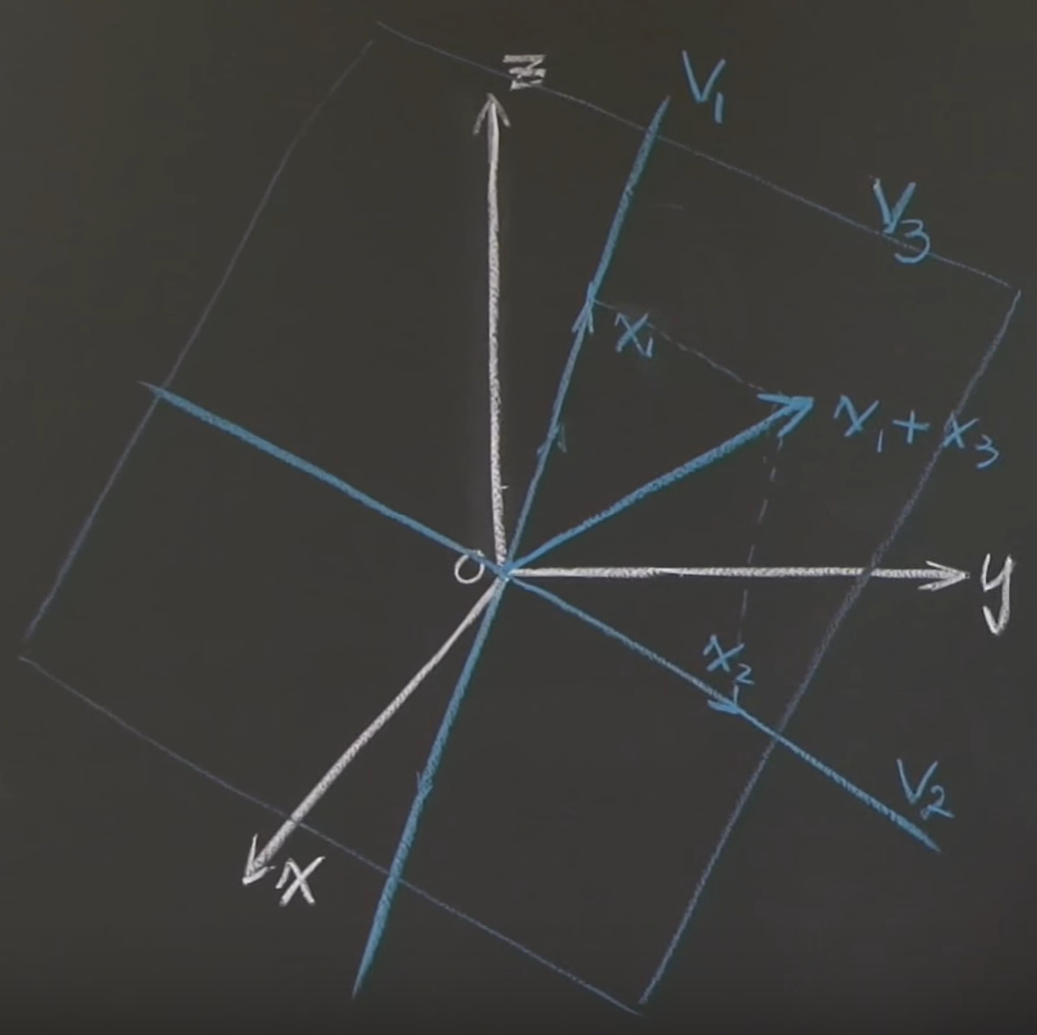
- $V_3$는 평면이다. 하지만 $V_1 \cup V_2$는 두 벡터 부분공간의 합집합일 뿐이다.
$$
x_3 =
\begin{bmatrix}
2 \\
5 \\
3 \\
\end{bmatrix} \notin V_1 \cup V_2
$$
Q3
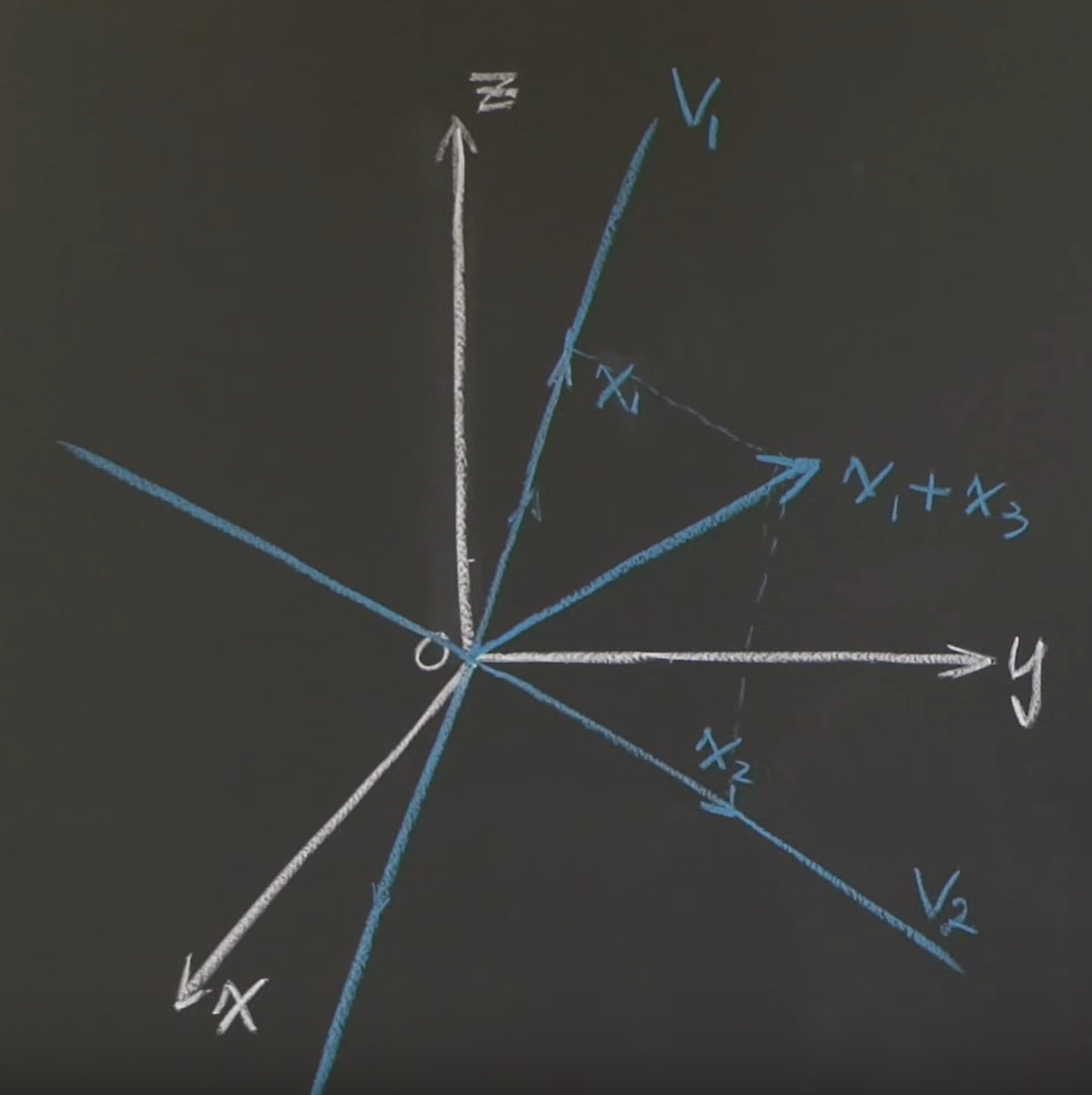
- 단순하게 $x_1 + x_2$가 생성하는 부분공간을 생각해보자.
- 그림에서 보듯이 이는 $V_1$ , $V_2$ 어디에도 속하지 않는다.
Q4
- 역시 그림에서 분명히 확인할 수 있다.
$V_3 \cap$ ($x-y$ plane$) = V_2$
Column Space and Null Space
https://www.youtube.com/watch?v=8o5Cmfpeo6g
$$
\underbrace{\mathbf A}_{m \times n} x = \{ 0 \}
$$
- $C(\mathbf A)$ is the vector space generated by columns of $\mathbf A$
- $C(\mathbf A) \in \mathbb R^m$
- $\mathcal N(\mathbf A)$ is the vector space generated by solution $x$ of $\mathbf A x = \mathbf 0$
- $\mathcal N(\mathbf A) \in \mathbb R^n$
$$
{\mathbf A} x = c,\text{~where } c \neq \mathbf 0
$$
- 위 식의 해 $x$는 벡터 공간일까? 당연히 아니다! 왜냐하면, $x =0$를 해로 지니지 못하기 때문이다.
- 매트릭스 형태로 표현된 연립방정식의 해는 벡터 공간이 될 수 없다.