Following Gilbert Strang 2
매트릭스 곱을 이해하는 4가지 방법 그리고 역행렬
Source
3. Multiplication and Inverse Matrices
4 Views of Matrix Multiplication
Standard
$$
\underbrace{ \mathbf A }_{m \times n} \underbrace{\mathbf B}_{n \times p} = {\mathbf C}
$$
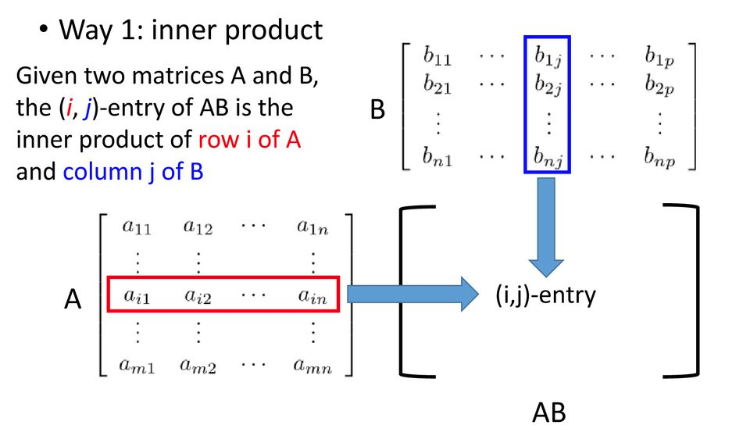
- $c_{ij}$는 뭘까? $\mathbf A$의 $i$ 행 벡터와 $\mathbf B$의 $j$ 열 벡터의 곱이다. 즉,
$$
c_{ij} = \sum_{k}^n a_{ik} b_{kj}
$$
Combination of Columns of A
$$
[A_1 \dotsc A_n]
\begin{bmatrix}
b_{11} \\
\vdots \\
b_{n1}
\end{bmatrix} = b_{11} A_1 + \dotsc + b_{n1} A_n = C_1
$$
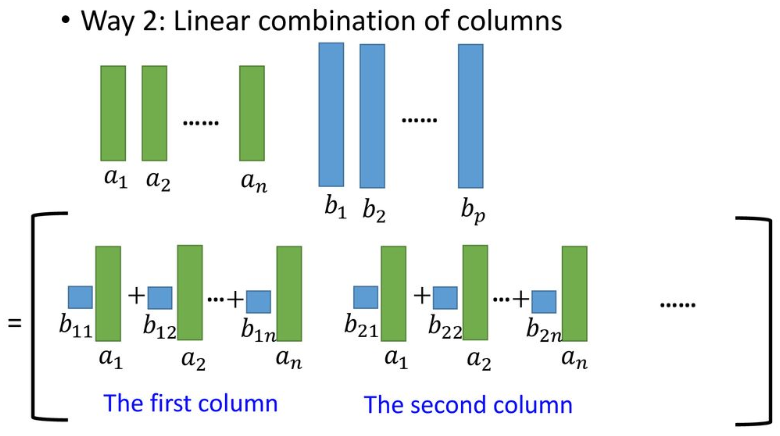
- 즉, 매트릭스 $A$의 열 벡터 $A_i$가 있을 때 이를 B의 각 열 벡터로 선형결합한 것이 $\mathbf C$의 각 열을 구성하게 된다.
$$
[A_1 \dotsc A_n]
\begin{bmatrix}
b_{1i} \\
\vdots \\
b_{ni}
\end{bmatrix} = b_{1i} A_1 + \dotsc + b_{ni} A_n = \text{col } C_i, \text{for } i = 1, \dotsc, p.
$$
$$
{\mathbf C} = [\text{col }C_1 \dotsc \text{col } C_p]
$$
Combination of Rows of B
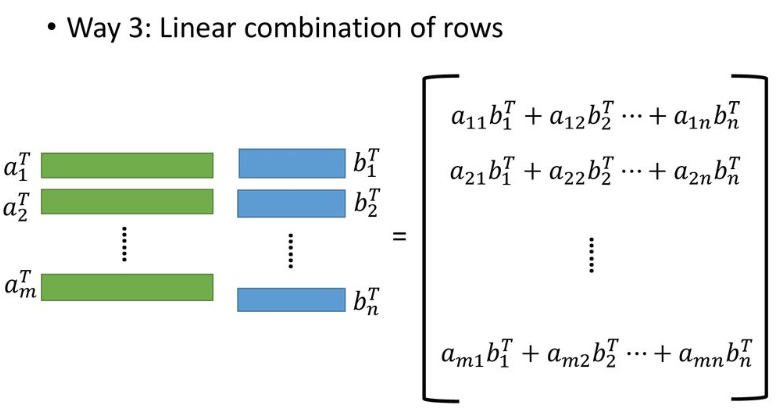
- 위의 해석과 거의 같다. 다만, $A$와 $B$의 역할을 바꾼 형태다. 즉,
$$
[a_{i1} \dotsc a_{in}]
\begin{bmatrix}
B_{1} \\
\vdots \\
B_{n}
\end{bmatrix} = a_{11} B_1 + \dotsc + a_{in} B_n = \text{row } C_i, \text{for } i = 1, \dotsc, m
$$
$$
{\mathbf C} =
\begin{bmatrix}
\text{row } C_1 \\
\vdots \\
\text{row } C_m
\end{bmatrix}
$$
Summation of Matices
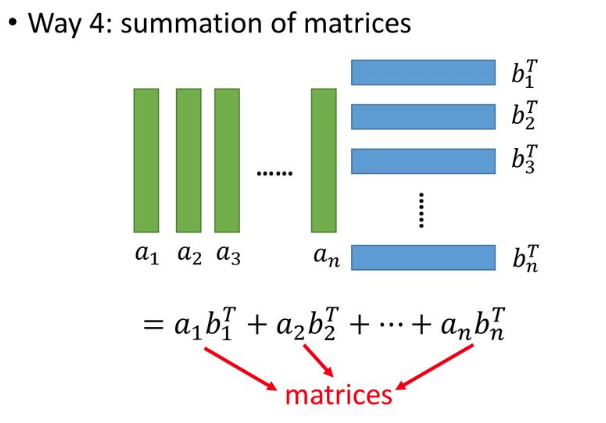
- 가장 급진적인 형태? 흥미롭게 생각해볼 수 있는 것은 각 개별 행렬의 rank다. 각각은 모두 1이다.
$$
[A_1 \dotsc A_n]
\begin{bmatrix}
B_{1} \\
\vdots \\
B_{n}
\end{bmatrix} = \underbrace{A_1 B_1}_{(m \times 1) \times (1 \times p)} + \dotsb + A_n B_n
$$
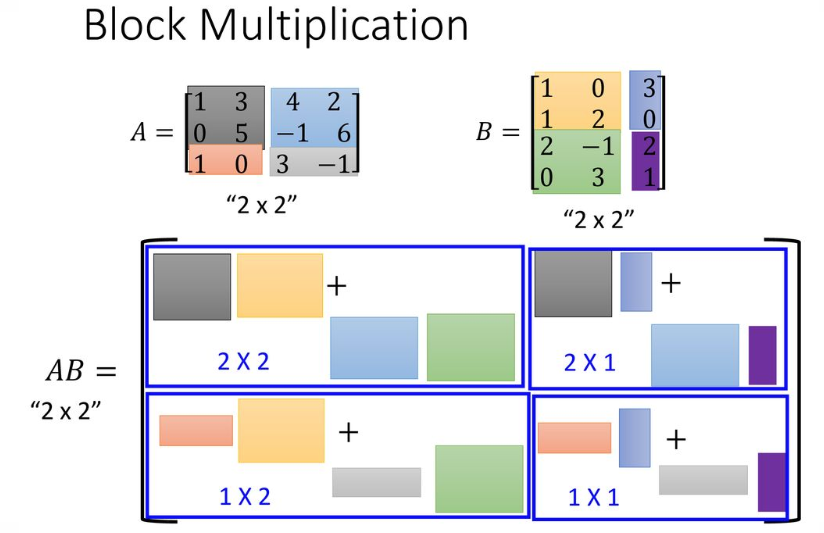
Block Multiplication
Inverse of Matrix
- 정의상 보면, 정방행렬 $A$에 대해서 역행렬 $A^{-1}$은
$$
{\mathbf A} {\mathbf A}^{-1} = {\mathbf I}, \text{ also } {\mathbf A}^{-1} {\mathbf A} = {\mathbf I}
$$
- 역행렬이 존재하는 정방행렬을 non-singluar or invertible matrices라고 부른다.
- singluar or non-invertible
- 역행렬을 구하는 과정을 따져보자.
$$
{\mathbf A} [A^{-1}_1, \dotsc A^{-1}_n] = {\mathbf I}
$$
- $A^{-1}_i$는 역행렬 ${\mathbf A}^{-1}$의 컬럼 벡터
- 역행렬을 구하는 문제는 사실 $n$개의 연립방정식을 푸는 문제와 구조상 동일하다.
Another definition
- ${\mathbf A} x = 0$를 만족하는 $0$ 벡터가 아닌 벡터 $x$가 존재하면 singular matrix.
- 증명은 간단하다.
- $\mathbf A$의 역행렬이 존재하고, $x \neq 0$라고 하자.
- ${\mathbf A}^{-1} {\mathbf A} x = {\mathbf A}^{-1} 0 = 0$
- 따라서 ${\mathbf I}x = {0}$이 되고, $x \neq 0$와 전제와 모순이다.
Singularity
- 만일 $\mathbf A$의 한 열이 모두 0이면 singular - 왜냐하면, 나머지 열을 조합하는 $x$의 원소를 0으로 놓고 해당 열을 조합하는 $x$는 0이 아닌 다른 숫자를 넣으면 $x \neq 0$인 ${\mathbf A} x = 0$를 얻을 수 있다.
- 만일 $\mathbf A$의 한 열과 다른 열이 스칼라 값을 곱해 구해진다면 singular - 비슷한 논리로 이해할 수 있다. 두 열을 제외한 다른 $x$의 원소를 0으로 두고 해당 두 열을 적절한 수로 곱하면, $x \neq 0$인 ${\mathbf A} x = 0$를 얻을 수 있다.
Using Gauss Jordan For Inverse Matices
$[{\mathbf A} \vert {\mathbf I}]$와 같은 형태의 augmented matrix를 만든 후, $\mathbf A$를 $\mathbf I$로 만드는 가우스-조르단 프로세스를 반복하면, $\mathbf I$ 자리에 ${\mathbf A}^{-1}$을 얻게 된다.
Example
$$
[{\mathbf A}|{\mathbf I}] =
\begin{bmatrix}
3 &-2 & 4 & \vert & 1 & 0 & 0\\
1 & 0 & 2 & \vert & 0 & 1 & 0\\
0 & 1 & 0 & \vert & 0 & 0 & 1\\
\end{bmatrix}
$$
- 첫번째 행과 두번째 행을 바꾼다.
$$
[{\mathbf A}|{\mathbf I}] \sim
{\tilde E}_{12} [{\mathbf A}|{\mathbf I}] =
\begin{bmatrix}
1 & 0 & 2 & \vert & 0 & 1 & 0 \\
3 &-2 & 4 & \vert & 1 & 0 & 0 \\
0 & 1 & 0 & \vert & 0 & 0 & 1
\end{bmatrix}
$$
- 두번째 행과 세번째 행을 바꾼다.
$$
[{\mathbf A}|{\mathbf I}] \sim
{\tilde E_{23}} [{\mathbf A}|{\mathbf I}] =
\begin{bmatrix}
1 & 0 & 2 & \vert & 0 & 1 & 0 \\
0 & 1 & 0 & \vert & 0 & 0 & 1\\
3 &-2 & 4 & \vert & 1 & 0 & 0
\end{bmatrix}
$$
- 첫번째 행에 $-3$을 곱하고 이를 세번째 행과 더한 후 세번째 행에 둔다.
$$
\begin{aligned}
[{\mathbf A}|{\mathbf I}] \sim
E_{13} [{\mathbf A}|{\mathbf I}] & =
\begin{bmatrix}
1 & 0 & 2 & \vert & 0 & 1 & 0 \\
0 & 1 & 0 & \vert & 0 & 0 & 1\\
3+(-3) &-2 + 0 & 4 + (-6)& \vert & 1 + 0 & 0 + (-3) & 0 + 0
\end{bmatrix} \\
& =
\begin{bmatrix}
1 & 0 & 2 & \vert & 0 & 1 & 0 \\
0 & 1 & 0 & \vert & 0 & 0 & 1\\
0 &-2 & -2 & \vert & 1 & -3 & 0
\end{bmatrix}
\end{aligned}
$$
- 두번째 행에 2를 곱한 후 이를 세번째 행에 더하여 세번째 행에 둔다.
$$
\begin{aligned}
[{\mathbf A}|{\mathbf I}] \sim
E_{23} [{\mathbf A}|{\mathbf I}] & =
\begin{bmatrix}
1 & 0 & 2 & \vert & 0 & 1 & 0 \\
0 & 1 & 0 & \vert & 0 & 0 & 1\\
0 + 0 &-2 + 2 & -2 + 0& \vert & 1 + 0 & -3 + 0 & 0 + 2
\end{bmatrix} \\
& =
\begin{bmatrix}
1 & 0 & 2 & \vert & 0 & 1 & 0 \\
0 & 1 & 0 & \vert & 0 & 0 & 1\\
0 & 0 & -2 & \vert & 1 & -3 & 2
\end{bmatrix}
\end{aligned}
$$
- 첫번째 행과 세번째 행을 더한 후 이를 첫번째 행에 둔다.
$$
\begin{aligned}
[{\mathbf A}|{\mathbf I}] \sim
E_{31} [{\mathbf A}|{\mathbf I}] & =
\begin{bmatrix}
1 + 0 & 0 + 0 & 2 + (-2) & \vert & 0 + 1 & 1 + (-3) & 0 + 2\\
0 & 1 & 0 & \vert & 0 & 0 & 1\\
0 & 0 & -2 & \vert & 1 & -3 & 2
\end{bmatrix} \\
& =
\begin{bmatrix}
1 & 0 & 0 & \vert & 1 & -2 & 2 \\
0 & 1 & 0 & \vert & 0 & 0 & 1\\
0 & 0 & -2 & \vert & 1 & -3 & 2
\end{bmatrix}
\end{aligned}
$$
- 세번째 행에 $-1/2$을 곱한다.
$$
\begin{aligned}
[{\mathbf A}|{\mathbf I}] \sim
E_{3} [{\mathbf A}|{\mathbf I}] & =
\begin{bmatrix}
1 & 0 & 0 & \vert & 1 & -2 & 2 \\
0 & 1 & 0 & \vert & 0 & 0 & 1\\
0 & 0 & -2 * (-\frac{1}{2}) & \vert & \frac{1}{2} & -3*(-\frac{1}{2}) & -\frac{2}{2}
\end{bmatrix} \\
& =
\begin{bmatrix}
1 & 0 & 0 & \vert & 1 & -2 & 2 \\
0 & 1 & 0 & \vert & 0 & 0 & 1\\
0 & 0 & 1 & \vert & -\frac{1}{2} & \frac{3}{2} & 1
\end{bmatrix} \\
& = [{\mathbf I} \vert {\mathbf A}^{-1}]
\end{aligned}
$$
- 이 식을 얻기 위한 가우스-조르단 프로세스는 $E_3 E_{31} E_{23} E_{13} {\tilde E_{23}} {\tilde E}_{12}$으로 나타낼 수 있다.
- 이 프로세스의 곱, 즉 위에 적은 것이 역행렬 ${\mathbf A}^{-1}$이다.