Vector Space

먼저 벡터 스페이스를 살펴보기 위해서 몇 가지 정의부터 보자.

  • $V$ is vector space
  • $\vec v \in V$
  • $W$ is vector subspace $W \subseteq V$
  • span: 벡터의 선형 결합을 통해 생성되는 벡터 집합 $\text{span}(\vec v_1, \dotsc, \vec v_n) = \{\vec v | \vec v = \alpha_1 \vec v_1 + \dotsb + \alpha_n \vec v_n, \alpha_i \in \mathbb R \}$

행렬 $M \in \mathbb R^{m \times n}$이 있다고 할 때

  • $\mathcal R(M) \subseteq \mathbb R^n$: $M$의 로우 스페이스, 즉 $M$의 행들의 모든 가능한 선형 결합이 나타내는 벡터 공간
$$ \mathcal R (M) \overset{\rm def}{=} \{ \vec v \in \mathbb R^n | \vec v = \vec w^T M \text{ for some } \vec w \in \mathbb R^m \} $$
  • $\mathcal C(M) \subseteq \mathbb R^m$: $M$의 컬럼 스페이스, 즉 $M$의 열들의 모든 가능한 선형 결합이 나타내는 벡터 공간
$$ \mathcal C (M) \overset{\rm def}{=} \{ \vec w \in \mathbb R^m | \vec w = M v \text{ for some } \vec v \in \mathbb R^n \} $$
  • $\mathcal N(M) \subseteq \mathbb R^n$: $M$의 널 스페이스. 즉, 오른쪽에 곱해졌을 때 $\vec 0_{m}$이 되는 벡터의 집합 $\mathcal N(M) \overset{\rm def}{=} \{ \vec v \in \mathbb R^n | M \vec v = \vec 0 \}$
  • $\mathcal N(M^T) \subseteq \mathbb R^n$: $M$의 좌 널 스페이스. 즉, 왼쪽에 곱해졌을 때 $\vec 0_{n}$이 되는 벡터의 집합
$$ \mathcal N(M^T) \overset{\rm def}{=} \{ \vec w \in \mathbb R^m | \vec w^T M = \vec 0^T \} $$

혹은

$$ \mathcal N(M^T) \overset{\rm def}{=} \{ \vec w \in \mathbb R^m | M^T \vec w = \vec 0 \} $$

$M$의 랭크는 컬럼 스페이스의 차원 그리고 로우 스페이스의 차원과 같다.

$$ r(M) = \dim(\mathcal R (M)) = \dim(\mathcal C(M)) $$

Checklist

Zero vector

벡터 스페이스가 되려면 $\vec 0$를 집합 내에 지니고 있어야 한다. 간단한 내용 같지만 참 중요하다. 일단 벡터 스페이스의 정의에서 $\alpha \vec v$가 들어가기 때문에 $\alpha=0$의 조건에 따라서 $\vec 0$는 포함되어야 한다. 생각해 볼만한 대목. 벡터 서브스페이스 역시 마찬가지로 $\vec 0$을 포함해야 한다. 2차원 벡터로 이야기한다면, $y = 2x + 1$ 같은 형태의 선은 벡터 (서브) 스페이스가 될 수 없다.

Subset vs subspace

부분집합은 원래 집합에 일정한 조건을 부여한 것이고, 이 점에서는 서브 스페이스 역시 부분 집합에 속한다. 다만 모든 부분 집합이 서브 스페이스가 되진 않는다. 이 점에서 서브 스페이스의 조건이 보다 제약적이다.

다음과 같은 두 방정식의 해를 비교해보자. $A \vec x = \vec b$, $A \vec x = \vec 0$

$A \vec v_1 = \vec b$와 $A \vec v_2 = \vec b$를 생각해보자. $A(\vec v_1 + \vec v_2)$는 원래의 벡터 스페이스에 들어 있는가?

$$ A(\vec v_1 + \vec v_2) = 2 \vec b $$

$\vec b = \vec 0$가 아니라면, $\vec v_1 + \vec v_2$는 해가 될 수 없다. 조금 더 자세하게 표현해보자.

$A \vec v = \vec b$의 해 공간은 다음과 같은 완전해의 집합이다.

$$ \{ \vec c + \vec v_n\} \text{ where }\vec v_n \in \mathcal N (A) $$

즉, 해 공간은 특수해(particular solution) $\vec c$와 널 스페이스에 속한 벡터의 합으로 구성된다. 해 공간의 원소 하나를 $\vec x_1 = \vec c + \vec v_1$이라고 하고 다른 하나를 $\vec x_2 = \vec c + \vec v_2$라고 하자. 이 둘을 더하면, $2 \vec c + \vec v_1 + \vec v_2$가 된다. 이것이 해 공간 안에 있어야 하는데, $\vec c \neq 0$이면 성립하지 않는다.

한편 $\mathcal N(M)$은 자연스럽게 벡터 공간을 이룬다. 더한 것도 $\vec 0$에 있고, 스칼라 곱 역시 마찬가지다. 참고로 아래에서 보겠지만, $\mathcal R(M)$, $\mathcal C(M)$, $\mathcal N(M)$, $\mathcal N(M^T)$를 네 개의 근본 서브 스페이스라고 부른다. 네 개는 밀접한 연관을 지니고 있다.

Solutions

이 기회에 해의 종류를 한번 살펴보고 넘어가자.

  1. Particular solution (특수해): RREF에서 free variables를 모두 0으로 두고 찾은 해를 뜻한다.
  2. Homogenous soution (일반해): 일반해는 널 스페이스에 속하는 해를 뜻한다. 즉, $A \vec x = 0$을 만족시키는 $\vec x$를 의미한다.
  3. Complete solution (완전해): 완전해란 특수해와 일반해를 더한 형태이다. 즉, $x_c = x_p + c_h$

이제 각각의 의미를 음미해보자.

$$ A \vec x = A x_c = A(x_p + x_h) = A x_p + A x_h = A x_p + \vec 0_{m} $$

보다 자세한 사례는 여기를 참고하라. 약간의 직관적인 설명만 곁들이겠다. 특수해는 딱 그 위치에 있어야 하는 벡터다. 즉 free variable이 어떤 값이 오건 간에 이 벡터의 값은 고정되어 있다. 반면 일반해는 널 스페이스에 속한다. 앞서 널 스페이스는 부분 공간이라고 말했다. 이는 $\vec 0$를 중심으로 각각 벡터가 지나가야 한다는 뜻이다. 따라서 free variable의 경우 하나를 구하기 위해서 나머지를 0으로 두고 구해야 한다. 그리고 이렇게 구해진 vector에 곱해지는 스칼라 값이 free variable에 해당한다.

System of Linear Equations

다음 방정식의 해 공간을 생각해보자.

$$ M \vec x = \vec b $$

먼저 $M$의 널 스페이스를 생각해보자. 여기 속한 $\vec x$는 $\mathbb R^n$ 집합에 속한다. 정의상 $M \vec x = 0$이므로 $\vec x$를 어떤 해에 더하면 이 값 역시 해가 된다. 따라서, $M \vec x = \vec b$를 만족하는 $\vec x = \vec c$라고 하자. 이를 특수 해라고 부른다. 여기에 널 스페이스에 속한 임의의 원소를 더하면 완전해가 된다. 즉,

$$ \vec x = \vec c + \text{span}(\vec v_1, \dotsc, \vec v_k) \text{ where } \text{span}(\vec v_1, \dotsc, \vec v_k) = \mathcal N(M) $$

RREF method

연립방정식의 해를 구하는 가장 기초적인 방법, 즉 RREF, 기약 행사다리꼴 행렬을 만드는 과정이 이에 부합한다. 즉, $[M \lvert \vec b]$를 RREF로 만들면, $[\text{rref}(M) \vert \vec c]$의 형태가 된다. 이때, $\text{rref}(M)$는 $k$ 개의 자유 변수를 $n-k$ 개의 특수 해를 지니게 된다. 자유 변수에서 널 스페이스에 속하는 일반해를 얻을 수 있다.

Two Transformation

$M \in \mathbb R^{m \times n}$이 편리한 이유는 $M$이 $\vec x \in \mathbb R^n$을 $\vec y \in \mathbb R^m$으로 바꾸는 선형 변환 모두를 표현할 수 있기 때문이다. 그렇다면, $M^T$는 어떨까? 이는 같은 맥락에서 $\vec a \in \mathbb R^m$을 $\vec b \in \mathbb R^n$으로 바꾸는 선형 변환을 표현한다. 즉,

$$ \vec a^T M = \vec b $$

이는 $M^T \vec a= \vec b$가 된다. 즉, $M^T$는 $M$의 좌 벡터 공간의 집합을 표현한다. 마찬가지로 $M$은 $M$의 우 벡터 공간의 집합을 표현한다. $M$의 좌 벡터 공간이 바로 로우 공간이고 우 벡터 공간이 컬럼 공간이다.

이제, $\mathcal N(M)$의 원소는 $\mathbb R^n$에 속한다. 이와 직교하는 공간은 어떤 공간일까? 좌 벡터 공간일까? 우 벡터 공간일까? 쉽게 생각하자. 직교 하기 위해서는 서로 차원이 같아야 한다. 우 벡터 공간은 $\mathbb R^m$에 속한다. 따라서 직교한다면 좌 벡터 공간과 한다. 확인해보자. $M \vec v_n = \vec 0_m$ where $\vec v_n \in \mathcal N(M)$ 가 성립한다. 이제 양번에 $\vec a^T$를 곱해보자.

$$ \underbrace{(M^T \vec a)^T}_{\text{left space}} \vec v_n = \vec a^T M\vec v_n = \vec a^T \vec 0_m = 0 $$
$$ \mathcal R(M) \oplus \mathcal N(M) = \mathbb R^n $$

한편 같은 논리로

$$ \mathcal C(M) \oplus \mathcal N(M^T) = \mathbb R^m $$

앞서 보았듯이 ${\rm rank} (M) =\dim(\mathcal R(M)) = \dim(\mathcal C(M))$다. $\dim(\mathcal N(M)) = {\rm nullity} (M)$이라고 하면,

$$ {\rm rank} (M) + {\rm nullity} (M) = n = \dim(\mathbb R^n) $$

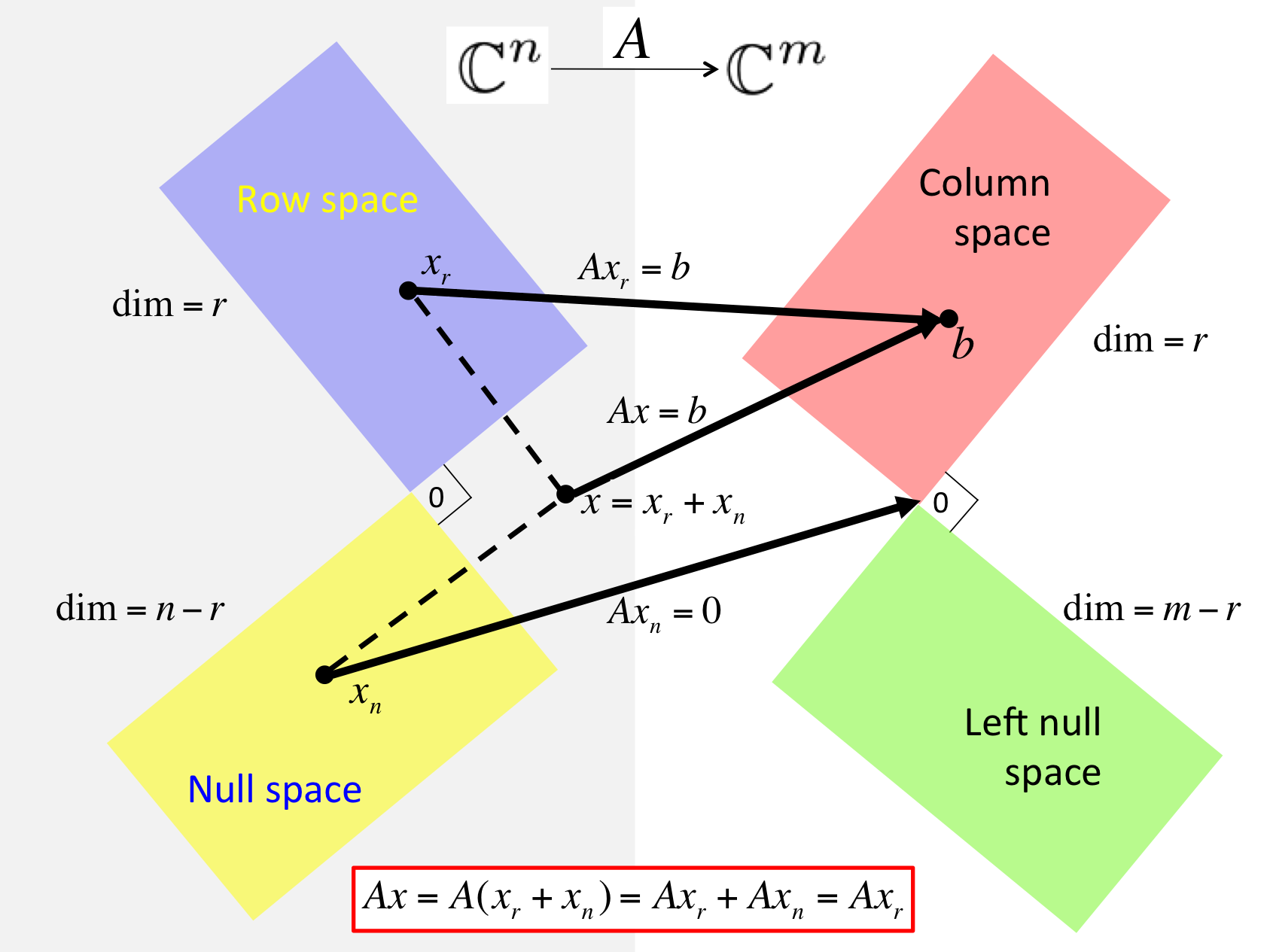
이 모든 걸 그림 하나로 정리하면 다음과 같다! 아래 보듯이 특수해(particular solution) $x_r$은 로우 스페이스에서 생성되는 해이다. 일반해(homogeneous solution) $x_n$은 널 스페이스에서 생성되는 해다.1 이 둘을 합치면 완전해(complete solution)가 된다. 아래 그림에서 보듯이

$$ \begin{aligned} Ax_r & \rightarrow \mathcal C(M) \\ Ax_n & \rightarrow \mathcal N(M) \\ Ax_c = A(x_r + x_n) & \rightarrow \mathcal C(M) \end{aligned} $$

enter image description here

  1. 보통 homogenous라는 말이 들어가면 $Ax = 0$과 같은 형태의 연립방정식을 의미 의미한다. ↩