tl;dr

  • 닷 프로덕트 혹은 내적을 기하적으로 이해하면 여러모로 편리하고 기억에도 잘 남는다.

Definition

dot product는 내적이라고도 번역하지만 여기서는 닷 프로덕트로 쓰기로 하겠다. 먼저 정의부터 살펴보자.

$$ \mathbf{u}=\left[u_{1}, {u}_{2}, \ldots, {u}_{n}\right] \in {\mathbb R}^n $$
$$ \mathbf{v}=\left[{v}_{1}, {v}_{2}, \ldots, {v}_{n}\right] \in {\mathbb R}^n $$
$$ \mathbf{u} \cdot \mathbf{v} = \sum_{n} u_i v_i $$

쉽게 말해서 닷 프로덕트는 차원이 같은 두 개의 인풋 벡터를 하나의 스칼라로 바꿔주는 일종의 함수로 이해할 수 있다. 두 개의 벡터를 서로 연관 짓는데 이를 해당 벡터의 길이라는 정보로 압축한다고 보면 얼추 맞을 듯 싶다. 하나의 숫자로 요약된다는 뜻에서 스칼라 프로덕트라고도 불린다. 그림으로 나타내면 아래와 같다.

From Definition to Geometry

닷 프로덕트에 관한 설명은 정의에서 바로 코사인 법칙으로 넘어간다. 하지만 뭔가 분명하지 않다. 이걸 조금 더 풀어보자.

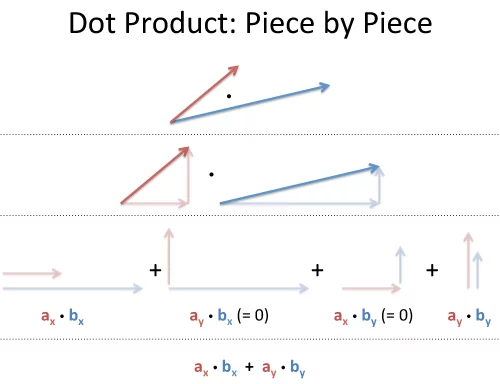
위 그림은 $2 \times 2$ 벡터의 닷 프로덕트를 각 요소로 분해한 것이다. 이중에서 $\dfrac{\pi}{2}$ 각을 이루고 있는 벡터는 서로 곱하면 0이 된다. 따라서 닷 프로덕트 계산에서는 $a_x b_x$와 $a_y b_y$가 남게 된다.

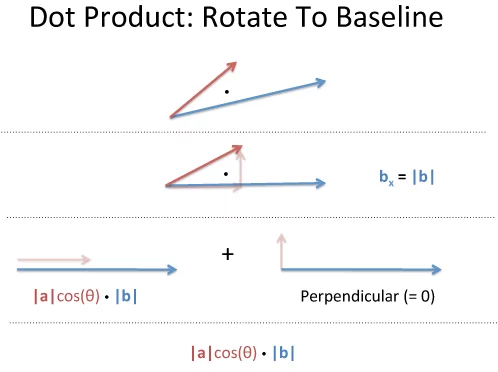
닷 프로덕트란 길이만 문제가 되므로 두 벡터를 한 방향으로 정렬하자.이렇게 되면, 파란색 높이가 $0$이 된다. 따라서 위 그림과 같은 코사인 법칙이 쉽게 도출된다.

Symmetry

$\mathbf{v}$ 벡터를 $\mathbf u$ 벡터 위에, 즉 이 벡터를 스크린 삼아 직각으로 쏜 프로젝션 벡터($\mathrm{Proj}_{\mathbf u}{\mathbf v}$)의 길이와 $\mathbf u$ 길이를 곱하면 그것이 $\mathbf u$와 $\mathbf v$의 닷 프로덕트가 된다. 어느 벡터로 프로젝션 하는지는 관계가 없다. 즉,

$$ {\mathbf v} \cdot {\mathbf u} = \Vert \mathbf u \Vert \Vert {\rm Proj}_{\mathbf u} {\mathbf v} \Vert = \Vert \mathbf u \Vert (\Vert \mathbf v \Vert \cos\theta) $$
$$ {\mathbf u} \cdot {\mathbf v} = \Vert \mathbf v \Vert \Vert {\rm Proj}_{\mathbf v} {\mathbf u} \Vert = \Vert \mathbf v \Vert (\Vert \mathbf u \Vert \cos\theta) $$

다시 보면, 닷 프로덕트의 정의상 ${\mathbf v} \cdot {\mathbf u} = {\mathbf u} \cdot {\mathbf v}$인 셈이다. 닷 프로덕트는 어떻게 도출하는가? 그 기하학적인 구조는 무엇인가?

With ‘Law of Cosine’

우선 정석부터 가보자. 코사인 법칙을 활용해서 닷 프로덕트를 도출할 수 있다. 1

우선 코사인의 법칙부터 살펴보자.

$$ \lVert \mathbf u - \mathbf v \rVert^2 = \lVert \mathbf u \rVert^2 + \lVert \mathbf v \rVert^2 - 2\lVert \mathbf u \rVert \lVert \mathbf v \rVert \cos \theta $$
  • 노름(norm, 길이)에 대해서는 대칭과 쌍방선형이 유지되기 때문에 아래와 같이 쓸 수 있다.
$$ \lVert \mathbf u - \mathbf v \rVert^2 = ( \mathbf u - \mathbf v) \cdot ( \mathbf u - \mathbf v ) = \lVert \mathbf u \rVert^2 + \lVert \mathbf v \rVert^2 - 2 (\mathbf u \cdot \mathbf v) $$

따라서

$$ \mathbf u \cdot \mathbf v = \lVert \mathbf u \rVert \lVert \mathbf v \rVert \cos \theta = \lVert \mathbf u \rVert ( \lVert \mathbf v \rVert \cos \theta) = \lVert \mathbf u \rVert \rVert \text{Proj}_{\mathbf u} \mathbf v \lVert $$

한편 반대로 $\mathbf u$에서 $\mathbf v$로 프로젝션하는 경우를 생각해 볼 수도 있겠다.

$$ \mathbf u \cdot \mathbf v = \lVert \mathbf u \rVert \lVert \mathbf v \rVert \cos \theta = \lVert \mathbf v \rVert ( \lVert \mathbf u \rVert \cos \theta) = \lVert \mathbf v \rVert \rVert \text{Proj}_{\mathbf v} \mathbf u \lVert $$

Applications

Cosine similarity

두 개의 벡터가 얼마나 유사한지를 나타내는 지표로 코사인 유사도라는 게 있다. 위에서 보듯이 두 개의 벡터($\mathbf v, \mathbf u$)가 이루는 각 $\theta$의 코사인 값은 다음과 같다.

$$ \cos \theta = \dfrac{\mathbf u \cdot \mathbf v}{\lVert \mathbf u \rVert \lVert \mathbf v \rVert} $$

두 벡터가 가까울수록 코사인 값이 1에 가깝게 될 것이고, 멀수록 -1에 가깝게 될 것이다.

Hyperplane

닷 프로덕트를 이해하고 있으면 기하학 문제를 쉽게 풀 수 있는 게 많다. 가장 좋은 예가 초평면(hyperplane)이다. 예를 들어 3차원 공간에서 점 $\mathbf{x}^0 = (x_1^0, x_2^0, x_3^0)$를 지나면서 벡터 $\mathbf{p} = (p_1, p_2, p_3)$에 수직인 평면을 찾고 있다고 하자. 복잡해보이지만 닷 프로덕트를 활용하면 쉽게 풀린다. 즉,

$$ \mathbf{p} \cdot (\mathbf{x} - \mathbf{x}^0) = 0 $$

평면 $\mathbf x$가 $\mathbf{x}^0$를 지나는 것은 분명하다. 이 평면이 $\mathbf{p}$에 수직이라는 것은 두 벡터의 닷 프로덕트가 0이 되면 된다.

Appendix: Geometrically

기하적으로 도출하는 보다 복잡한 방법도 있다.2 이해를 돕기 위해서 2차원 벡터공간으로 한정해서 논의하겠다. $n$ 차원으로 확대하는 것이 수학적으로 어렵지는 않다.

일단 $\mathbf u$가 길이 1로 표준화된 벡터라고 정의를 살짝 바꾸겠다. 즉, 새로운 $\mathbf u$는 $\rVert \mathbf u \lVert$로 $\mathbf u$를 나눈 벡터다. 아래 그림처럼 이 벡터를 향해서 2차원 평면의 기저를 구성하는 $(1,0)(\equiv i)$과 $(0,1)(\equiv j)$에서 벡터로 프로젝션을 해보자.

이렇게 프로젝션을 하면 프로젝션된 지점의 $x$ 좌표는 공교롭게도 원점에서부터 해당 프로젝션된 지점까지의 벡터의 길이가 된다. $y$에 대해서도 마찬가지다.

이제 (1,1)에서 벡터 $\mathbf u$로 프로젝션을 해보자. (1,1)은 각각 두 개의 기저를 1의 가중치로 선형결합한 벡터다. 이 벡터의 프로젝션의 길이는 어떻게 구성될까? 그림에서 보듯이 $u_x + u_y$가 된다. 이를 일반적인 논리로 확장해보자. 어떤 임의의 벡터 $\mathbf v(=(x,y))$가 존재할 때 해당 벡터는 각각 두 개의 기저의 선형 결합으로 이해할 수 있다.

따라서 $\mathbf v$ 벡터를 $\mathbf u$로 프로젝션한 길이는 다음과 같다.

$$ \underset{\mathbf u 프로젝션}{\left[\begin{array}{ll}{u_{x}} & { u_{y}}\end{array}\right]}\left[\begin{array}{l}{x} \\ {y}\end{array}\right]= u_{x} \cdot x + u_{y} \cdot y = \mathbf u \cdot \mathbf v $$

벡터를 기저의 선형결합을 통해 나타낼 수 있듯이, 벡터의 프로젝션의 길이 역시 비슷한 방식의 선형결합을 동원해서 나타낼 수 있다. 앞서 $\mathbf u$가 표준화된 벡터라고 했다. 따라서 원래대로 돌려 놓으면 닷 프로덕트는 프로젝션된 지점까지의 벡터의 거리와 해당 벡터의 길이의 곱이 된다. 즉,

$\mathbf u \cdot \mathbf v = \rVert \mathbf u \lVert \rVert \text{Proj}_{\mathbf u} \mathbf v \lVert$

  1. 여기를 참고 했다. ↩

  2. 보다 상세한 내용은 여기를 참고하라. ↩